Answer:
the expected area of the resulting circular region is 616.38 m²
Explanation:
Given that:
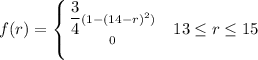 otherwise
otherwise
The expected area of the resulting circular region is:
=
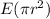
=
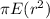
To calculate
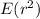
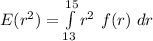
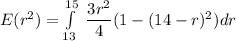
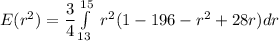
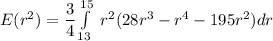
![E(r^2) = (3)/(4)[(28 r^4)/(4)-(r^5)/(5)-(195r^3)/(3)]^{^(15)}}__(13)](https://img.qammunity.org/2021/formulas/mathematics/college/14cw5qbanbv6jzzt27q3z43mvja6f6yk0z.png)
![E(r^2) = (3)/(4) [ (28 * 50625)/(4) - (759375)/(5) - (195 * 3375)/(3) ]-[ (28 * 28561)/(4) - (371293)/(5) - (195 * 2197)/(3) ]](https://img.qammunity.org/2021/formulas/mathematics/college/c2b0nu8wrew5wsaoqg8hqdp3yq2o90gelt.png)
![E(r^2) = (3)/(4) [ 354375-151875-219375-199927+74258.6+142805]](https://img.qammunity.org/2021/formulas/mathematics/college/p9o9653eimxjs8iv5y9d7ofpqu8cc7l358.png)
![E(r^2) = (3)/(4) [261.6]](https://img.qammunity.org/2021/formulas/mathematics/college/86jocb9072c66v1hbs9ekqnon4csefv5js.png)
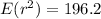
Recall:
The expected area of the resulting circular region is:
=
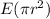
=
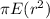
where;
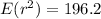
Then
The expected area of the resulting circular region is:
=
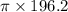
= 616.38 m²