Answer:
3.6°
Explanation:
The question is incomplete. Here is the complete question.
Find the angle between the given vectors to the nearest tenth of a degree.
u = <8, 7>, v = <9, 7>
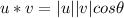
we will be using the formula below to calculate the angle between the two vectors;
is the angle between the two vectors.
u = 8i + 7j and v = 9i+7j
u*v = (8i + 7j )*(9i + 7j )
u*v = 8(9) + 7(7)
u*v = 72+49
u*v = 121
|u| = √8²+7²
|u| = √64+49
|u| = √113
|v| = √9²+7²
|v| = √81+49
|v| = √130
Substituting the values into the formula;
121= √113*√130 cos θ
cos θ = 121/121.20
cos θ = 0.998
θ = cos⁻¹0.998
θ = 3.6° (to nearest tenth)
Hence, the angle between the given vectors is 3.6°