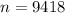Question

TV advertising agencies face increasing challenges in reaching audience members because viewing TV programs via digital streaming is gaining in popularity. A poll reported that 54% of 2348 American adults surveyed said they have watched digitally streamed TV programming on some type of device.

1) Calculate and interpret a confidence interval at the 99% confidence level for the proportion of all adult Americans who watched streamed programming up to that point in time.
A) We are 99% confident that this interval does not contain the true population proportion.
B) We are 99% confident that this interval contains the true population proportion.
C) We are 99% confident that the true population proportion lies below this interval.
D) We are 99% confident that the true population proportion lies above this interval.
2) What sample size would be required for the width of a 99% CI to be at most 0.03 irrespective of the value of p?

Answer 1

1

Option B is the correct answer

2

`n = 9418`

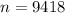
Explanation:

From the question we are told that

The sample size is
`n = 2348`

The sample proportion is
`\r p = 0.54`

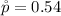
Given that the confidence level is 99% then the level of significance is evaluated as

`\alpha = 100 - 99`

`\alpha = 1`%

`\alpha = 0.01`

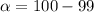
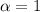Next we obtain the critical values of
`(\alpha )/(2)` from the normal distribution table. The values obtained is

`Z_{(\alpha )/(2) } = 2.58`

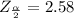
The reason we are obtaining values for is because is the area under the normal distribution curve for both the left and right tail where the 99% interval did not cover while is the area under the normal distribution curve for just one tail and we need the value for one tail in order to calculate the confidence interval .

Next is to calculate the margin of error which is mathematically evaluated as

`MOE = Z_{(\alpha )/(2) } * \sqrt{ (\r p ( 1 - \r p ))/(n ) }`

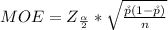
substituting values

`MOE = 2.58 * \sqrt{ (0 .54( 1 - 0.54 ))/(2348 ) }`

`MOE = 0.0265`

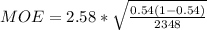
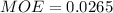
Now the interval for the 99% confidence level is evaluated as

`\r p - MOE < \r p < \r p + MOE`

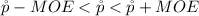
substituting values

`0.514 < \r p <0.567`

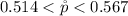
Looking at the Confidence interval we see that the proportion of Americans that watched streamed program up to that point in time is between

51.4% and 56.7%

Hence we are 99% confident that this interval contains the true population proportion.

The sample size that will be required for the width o 99% Cl is mathematically evaluated as

`n = \frac{4 *[Z_{(\alpha )/(2) }]^2 * \r p (1- \r p )}{MOE^2}`

substituting values

`n = (4 *2.58^2 * 0.54 (1- 0.54 ))/(0.0265^2)`

`n = 9418`