Question

The mean breaking strength of yarn used in manufacturing drapery material is required to be at least 100 psi. Past experience has indicated that the standard deviation of breaking strength is 2.6 psi. A random sample of 9 specimens is tested, and the average breaking strength is found to be 100.6 psi. Test the hypothesis that the mean breaking strength is larger than 100 psi by setting up the null and alternative hypotheses. Use alpha = .05.

a) What is the numerical value of your test statistic, z0?
b) What is the p-value resulting from the test of Part A? Answer to three decimal places.
c) What is the probability of Type II error for the hypothesis test of Part A if the true population mean is 101.3 psi? Answer to three decimal places

Answer 1

Explanation:

Given that:

Mean μ= 100

standard deviation σ = 2.6

sample size n = 9

sample mean X = 100.6

The null hypothesis and the alternative hypothesis can be computed as follows:

`H_o : \mu \leq 100`

`H_1 :\mu > 100`

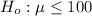
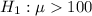
The numerical value for the test statistics is :

`z = (x - \mu)/((\sigma)/(√(n)))`

`z = (100.6- 100)/((2.6)/(√(9)))`

`z = (0.6)/(0.8667)`

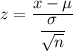
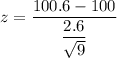
z = 0.6923

At ∝ = 0.05

`t_(\alpha/2 ) = 0.025`

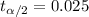
The critical value for the z score = 0.2443

From the z table, area under the curve, the corresponding value which is less than the significant level of 0.05 is 1.64

P- value = 0.244

c> If the true population mean is 101.3 ;

Then:

`z = (x - \mu)/((\sigma)/(√(n)))`

`z = (101.3- 100.6)/((2.6)/(√(9)))`

`z = (0.7)/(0.8667)`

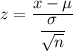
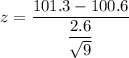
z = 0.808

From the normal z tables

P value = 0.2096