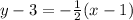Answer:

Explanation:
Point-slope is:


Our goal:
We have to complete the point-slope equation of the line through (1,3) (5,1).
--------------------------------------------------------
We have a incomplete equation of the line.
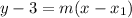
We need to find the slope of the line, and the value of
 .
.
--------------------------------------------------------
Finding 'x1':
It seems that the value of 3 was used to be
 . This means that the point
. This means that the point
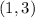 was used for the equation. This means that
was used for the equation. This means that
 would have to be 1.
would have to be 1.
Finding Slope:
Slope is rise over run.
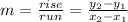
We are given the points (1,3) and (5,1).
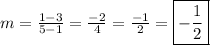
The slope is one-half.
--------------------------------------------------------
We now have enough information to complete the point-slope equation.
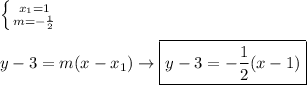
Our final equation is: