Question

A carpenter makes wooden chairs. He has enough wood to make 30 chairs. He makes $60 profit on a dining chair and $90 profit on a rocking chair. It takes him 1 hour to make a dining chair and 2 hours to make a rocking chair. He only has 40 hours available to work on the chairs. The carpenter wants to maximize his profit given the constraints. He draws the graph below to represent this situation. Drag and drop the correct numbers to complete the statements below. Given the restraints, the carpenter can maximize profits by making Response area dining chairs and Response area rocking chairs. His total profit for all the chairs will be $Response area.

Answer 1

The carpenter can maximize profits by making 20 dining chairs and 10 rocking chairs . His total profit for all the chairs will be $2100

Explanation:

Let x be the no. of dining chairs and y be the no. of rocking chair

Time taken by carpenter to make 1 dining chair = 1 hour

Time taken by carpenter to make x dining chairs = x hours

Time taken by carpenter to make 1 rocking chair = 2 hour

Time taken by carpenter to make y rocking chairs = 2y hours

He only has 40 hours available to work on the chairs.

`\Rightarrow x+2y \leq 40`

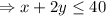
He has enough wood to make 30 chairs.

`\Rightarrow x+y\leq30`

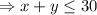
He makes $60 profit on a dining chair and $90 profit on a rocking chair.

So, profit =60x+90y

Plot the equations on graph

Refer the attached figure

Coordinates of feasible region

(0,20),(20,10) and (30,0)

Profit =60x+90y

At(0,20)

Profit = 1800

At(20,10)

Profit = 1200+900=2100

At(30,0)

Profit=900

So,the carpenter can maximize profits by making 20 dining chairs and 10 rocking chairs . His total profit for all the chairs will be $2100