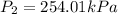Question

At one point in a pipeline, the water's speed is 3.57 m/s and the gauge pressure is 68.7 kPa. Find the gauge pressure at a second point in the line, 18.5 m lower than the first, if the pipe diameter at the second point is twice that at the first. Remember that the density of water is 1000 kg/m3. Please give your answer in units of kPa.

Answer 1

The pressure at point 2 is
`P_2 = 254.01 kPa`

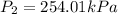
Step-by-step explanation:

From the question we are told that

The speed at point 1 is
`v_1 = 3.57 \ m/s`

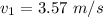
The gauge pressure at point 1 is
`P_1 = 68.7kPa = 68.7*10^(3)\ Pa`

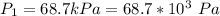
The density of water is
`\rho = 1000 \ kg/m^3`

Let the height at point 1 be
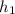`h_1` then the height at point two will be

`h_2 = h_1 - 18.5`

Let the diameter at point 1 be
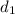`d_1` then the diameter at point two will be

`d_2 = 2 * d_1`

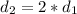
Now the continuity equation is mathematically represented as

`A_1 v_1 = A_2 v_2`

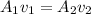
Here
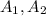`A_1 , A_2` are the area at point 1 and 2

Now given that the are is directly proportional to the square of the diameter [i.e
`A= (\pi d^2)/(4)`]

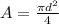which can represent as

`A \ \ \alpha \ \ d^2`

=>
`A = c d^2`

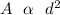
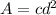
where c is a constant

so
`(A_1)/(d_1^2) = (A_2)/(d_2^2)`

=>
`(A_1)/(d_1^2) = (A_2)/(4d_1^2)`

=>
`A_2 = 4 A_1`

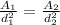
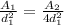
Now from the continuity equation

`A_1 v_1 = 4 A_1 v_2`

=>
`v_2 = (v_1)/(4)`

=>
`v_2 = (3.57)/(4)`

`v_2 = 0.893 \ m/s`

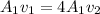
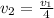
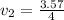
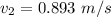
Generally the Bernoulli equation is mathematically represented as

`P_1 + (1)/(2) \rho v_1^2 + \rho * g * h_1 = P_2 + (1)/(2) \rho v_2^2 + \rho * g * h_2`

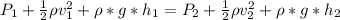
So

`P_2 = \rho * g (h_1 -h_2 )+P_1 + (1)/(2) * \rho (v_1^2 -v_2 ^2 )`

=>
`P_2 = \rho * g (h_1 -(h_1 -18.3) + P_1 + (1)/(2) * \rho (v_1^2 -v_2 ^2 )`

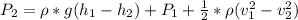
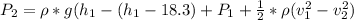
substituting values

`P_2 = 1000 * 9.8 (18.3) )+ 68.7*10^(3) + (1)/(2) * 1000 ((3.57)^2 -0.893 ^2 )`

`P_2 = 254.01 kPa`