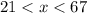Answer:
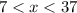 -- Triangle 1
-- Triangle 1
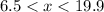 -- Triangle 2
-- Triangle 2
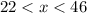 -- Triangle 3
-- Triangle 3
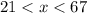 -- Triangle 4
-- Triangle 4
Explanation:
Given
2 sides of a triangle
1. 22 and 15
2. 13.2 and 6.7
3. 34 and 12
4. 23 and 44
Required
Determine the range of the third side in the above triangles
Triangle 1: 22 and 15
Represent the third side with x
We'll make use of the following conditions to calculate the range of the third side;
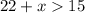
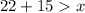
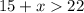
Solving
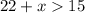
Make x the subject of formula
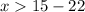
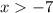
Solving
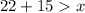
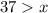
Solving
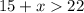
Make x the subject of formula
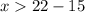
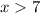
The next step is to dismiss the inequality with negative digit; So, we're left with
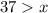 and
and
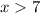
Rewrite both inequalities
 and
and
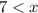
Combine the two inequalities
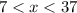
Triangle 2: 13.2 and 6.7
Represent the third side with x
We'll make use of the following conditions to calculate the range of the third side;
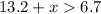
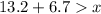
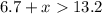
Solving
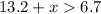
Make x the subject of formula
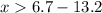

Solving
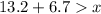
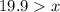
Solving
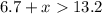
Make x the subject of formula
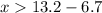
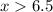
The next step is to dismiss the inequality with negative digit; So, we're left with
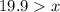 and
and
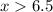
Rewrite both inequalities
 and
and
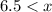
Combine the two inequalities
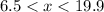
Triangle 3: 34 and 12
Represent the third side with x
We'll make use of the following conditions to calculate the range of the third side;
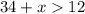

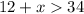
Solving
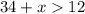
Make x the subject of formula
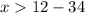
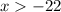
Solving

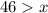
Solving
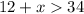
Make x the subject of formula
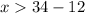

The next step is to dismiss the inequality with negative digit; So, we're left with
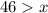 and
and

Rewrite both inequalities
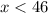 and
and
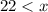
Combine the two inequalities
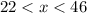
Triangle 4: 23 and 44
Represent the third side with x
We'll make use of the following conditions to calculate the range of the third side;
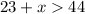
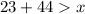
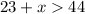
Solving
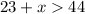
Make x the subject of formula
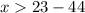

Solving
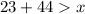
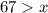
Solving
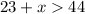
Make x the subject of formula
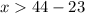

The next step is to dismiss the inequality with negative digit; So, we're left with
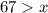 and
and

Rewrite both inequalities
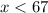 and
and
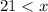
Combine the two inequalities