Answer:
(a)
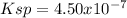
(b)

(c)
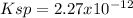
(d)
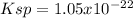
Step-by-step explanation:
Hello,
In this case, given the solubility of each salt, we can compute their molar solubilities by using the molar masses. Afterwards, by using the mole ratio between ions, we can compute the concentration of each dissolved and therefore the solubility product:
(a)
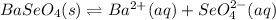
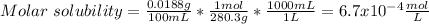
In such a way, as barium and selenate ions are in 1:1 molar ratio, they have the same concentration, for which the solubility product turns out:
![Ksp=[Ba^(2+)][SeO_4^(2-)]=(6.7x10^(-4)(mol)/(L) )^2\\\\Ksp=4.50x10^(-7)](https://img.qammunity.org/2021/formulas/chemistry/college/om4mkmkcujv90a5pd0r411fybyovi58fdt.png)
(B)
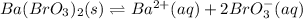
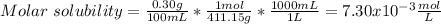
In such a way, as barium and bromate ions are in 1:2 molar ratio, bromate ions have twice the concentration of barium ions, for which the solubility product turns out:
![Ksp=[Ba^(2+)][BrO_3^-]^2=(7.30x10^(-3)(mol)/(L))(3.65x10^(-3)(mol)/(L))^2\\\\Ksp=1.55x10^(-6)](https://img.qammunity.org/2021/formulas/chemistry/college/4n8bu4rrnb8nzh39mpar8573p7rr80r8rp.png)
(C)
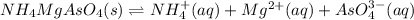

In such a way, as ammonium, magnesium and arsenate ions are in 1:1:1 molar ratio, they have the same concentrations, for which the solubility product turns out:
![Ksp=[NH_4^+][Mg^(2+)][AsO_4^(3-)]^2=(1.31x10^(-4)(mol)/(L))^3\\\\Ksp=2.27x10^(-12)](https://img.qammunity.org/2021/formulas/chemistry/college/5zatvv634paw59irgvz56u9h1kb5hqdnff.png)
(D)
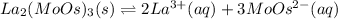
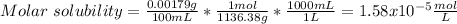
In such a way, as the involved ions are in 2:3 molar ratio, La ion is twice the molar solubility and MoOs ion is three times it, for which the solubility product turns out:
![Ksp=[La^(3+)]^2[MoOs^(-2)]^3=(2*1.58x10^(-5)(mol)/(L))^2(3*1.58x10^(-5)(mol)/(L))^3\\\\Ksp=1.05x10^(-22)](https://img.qammunity.org/2021/formulas/chemistry/college/dcnxepvh68mfmx4kdiz37cf5o1mi9cwhyb.png)
Best regards.