Answer:
Explanation:
From the information given:
Mean

Mean
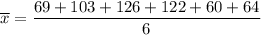
Mean
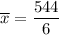
Mean
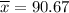 pounds
pounds
Standard deviation

Standard deviation
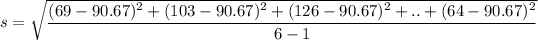
Standard deviation s = 30.011 pounds
B) Find a 75% confidence interval for the population average weight of all adult mountain lions in the specified region.
At 75% confidence interval ; the level of significance ∝ = 1 - 0.75 = 0.25
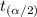 = 0.25/2
= 0.25/2
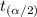 = 0.125
= 0.125
t(0.125,5)=1.30
Degree of freedom = n - 1
Degree of freedom = 6 - 1
Degree of freedom = 5
Confidence interval =
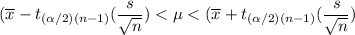
Confidence interval =

Confidence interval =

Confidence interval =

Confidence interval =
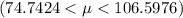
i.e the lower limit = 74.74 pounds
the upper limit = 106.60 pounds