Answer: lower bound = 0.7404; upper bound = 0.8596
Explanation:
The proportion p for this population:
p =
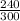
p = 0.8
Confidence interval for proportion is calculated as:
p ± z-score.
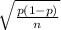
Z-score for a 99% confidence interval is: z = 2.58
Calculating:
0.8 ± 2.58.
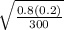
0.8 ± 2.58.
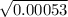
0.8 ± 2.58(0.0231)
0.8 ± 0.0596
This means that the lower limit of this interval is 0.7404 and upper bound is 0.8596