Question

The daily revenue at a university snack bar has been recorded for the past five years. Records indicate that the mean daily revenue is $2700 and the standard deviation is $400. The distribution is skewed to the right due to several high volume days (football game days). Suppose that 100 days are randomly selected and the average daily revenue computed. According to the Central Limit Theorem, which of the following describes the sampling distribution of the sample mean?

a. Normally distributed with a mean of $2700 and a standard deviation of $40
b. Normally distributed with a mean of $2700 and a standard deviation of $400
c. Skewed to the right with a mean of $2700 and a standard deviation of $400
d. Skewed to the right with a mean of $2700 and a standard deviation of $40

Answer 1

a. Normally distributed with a mean of $2700 and a standard deviation of $40

Explanation:

Given that:

the mean daily revenue is $2700

the standard deviation is $400

sample size n is 100

According to the Central Limit Theorem, the sampling distribution of the sample mean can be computed as follows:

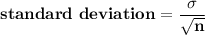
`\mathbf{standard \ deviation =( \sigma)/(√(n))}`

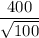
standard deviation =
`(400)/(√(100))`

standard deviation =
`(400)/(10)}`

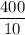
standard deviation = 40

This is because the sample size n is large ( i,e n > 30) as a result of that the sampling distribution is normally distributed.

Therefore;

the statement that describes the sampling distribution of the sample mean is : option A.

a. Normally distributed with a mean of $2700 and a standard deviation of $40