Question

Cincinnati Paint Company sells quality brands of paints through hardware stores throughout the United States. The company maintains a large sales force whose job it is to call on existing customers as well as look for new business. The national sales manager is investigating the relationship between the number of sales calls made and the miles driven by the sales representative. Also, do the sales representatives who drive the most miles and make the most calls necessarily earn the most in sales commissions? To investigate, the vice president of sales selected a sample of 25 sales representatives and determined:

%u2022 The amount earned in commissions last month (Y).
%u2022 The number of miles driven last month (X2)
%u2022 The number of sales calls made last month (X1)
($000) Calls Driven Commissions
($000) Calls Driven
22 139 2,371 38 146 3,290
13 132 2,226 44 144 3,103
33 144 2,731 29 147 2,122
38 142 3,351 38 144 2,791
23 142 2,289 37 149 3,209
47 142 3,449 14 131 2,287
29 138 3,114 34 144 2,848
38 139 3,342 25 132 2,690
41 144 2,842 27 132 2,933
32 134 2,625 25 127 2,671
20 135 2,121 43 154 2,988
13 137 2,219 34 147 2,829
47 146 3,463
Click here for the Excel Data File
Develop a regression equation including an interaction term. (Round your answers to 3 decimal places. Negative amounts should be indicated by a minus sign.)
Commissions = + Calls + Miles - X1X2
Complete the following table. (Round your answers to 3 decimal places. Negative amounts should be indicated by a minus sign.)
Predictor Coef SE Coef T P
Constant
Calls
Miles
X1X2
Compute the value of the test statistic corresponding to the interaction term. (Round your answer to 2 decimal places. Negative amount should be indicated by a minus sign.)
Value of the test statistic
Is there a significant interaction between the number of sales calls and the miles driven?

Answer 1

There is no significant interaction between the number of sales calls and the miles driven.

Explanation:

The variables are defined as follows:

Dependent (Y) = amount earned in commissions last month

Independent (X₁) = number of miles driven last month

Independent (X₂) = number of sales calls made last month

In this case we need to test whether there is a significant interaction between the number of sales calls and the miles driven.

The hypothesis can be defined as follows:

H₀: There is no significant interaction.

Hₐ: There is a significant interaction.

Assume that the significance level of the test is, α = 0.05.

Use the Data Analysis tool in Excel to form the regression equation.

For the regression equation, we need to compute the values of (X₁ × X₂).

Steps:

1. Go to Data - Data Analysis - Regression. A dialog box will open.
2. Select the Y values in the "Input Y range" and values of X₁, X₂ and X₁ × X₂ in the "Input X range".
3. Click OK.

The output of the regression analysis is attached below.

The regression equation is:

`Y=-455.07+3.128\cdot X_(1)+0.143\cdot X_(2)-0.001\cdot X_(1)X_(2)`

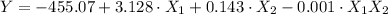
Consider the third table in the regression output.

The test statistic corresponding to the interaction term is:

t = -1.85

The p-value for the test of the interaction term is:

p-value = 0.078.

The p-value of the test is more than the significance value.

The null hypothesis will not be rejected.

Thus, concluding that there is no significant interaction between the number of sales calls and the miles driven.