Answer:
The sample size must be 45 large enough that would ensure that the first probability in part (a) is at least 0.99.
Explanation:
We are given that the sediment density (g/cm) of a randomly selected specimen from a certain region is normally distributed with mean 2.68 and standard deviation 0.92.
Let
 = sample average sediment density
= sample average sediment density
The z-score probability distribution for the sample mean is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = population mean = 2.68
= population mean = 2.68
 = population standard deviation = 0.92
= population standard deviation = 0.92
n = sample of specimens = 25
(a) The probability that the sample average sediment density is at most 3.00 is given by = P(

 3.00)
3.00)
P(

 3.00) = P(
3.00) = P(


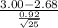 ) = P(Z
) = P(Z
 1.74) = 0.9591
1.74) = 0.9591
The above probability is calculated by looking at the value of x = 1.74 in the z table which has an area of 0.9591.
Also, the probability that the sample average sediment density is between 2.68 and 3.00 is given by = P(2.68 <
 < 3.00)
< 3.00)
P(2.68 <
 < 3.00) = P(
< 3.00) = P(
 < 3.00) - P(
< 3.00) - P(

 2.68)
2.68)
P(
 < 3.00) = P(
< 3.00) = P(
 <
<
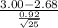 ) = P(Z < 1.74) = 0.9591
) = P(Z < 1.74) = 0.9591
P(

 2.68) = P(
2.68) = P(


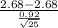 ) = P(Z
) = P(Z
 0) = 0.50
0) = 0.50
The above probability is calculated by looking at the value of x = 1.74 and x = 0 in the z table which has an area of 0.9591 and 0.50.
Therefore, P(2.68 <
 < 3.00) = 0.9591 - 0.50 = 0.4591.
< 3.00) = 0.9591 - 0.50 = 0.4591.
(b) Now, we have to find a sample size that would ensure that the first probability in part (a) is at least 0.99, that is;
P(

 3.00)
3.00)
 0.99
0.99
P(


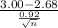 )
)
 0.99
0.99
P(Z

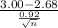 )
)
 0.99
0.99
Now, in the z table; the critical value of x which has an area of at least 0.99 is given by 2.3263, that is;
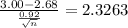

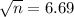
n = 44.76 ≈ 45 {By squaring both sides}
Hence, the sample size must be 45 large enough that would ensure that the first probability in part (a) is at least 0.99.