Question

Find all x in set of real numbers R Superscript 4 that are mapped into the zero vector by the transformation Bold x maps to Upper A Bold x for the given matrix A.

Answer 1

`x_3 = \left[\begin{array}{c}4&3&1\\0\end{array}\right]`

Explanation:

According to the given situation, The computation of all x in a set of a real number is shown below:

First we have to determine the
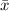`\bar x` so that
`A \bar x = 0`

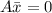
`\left[\begin{array}{cccc}1&-3&5&-5\\0&1&-3&5\\2&-4&4&-4\end{array}\right]`

Now the augmented matrix is

`\left[\begin{array}{cccc}1&-3&5&-5\ |\ 0\\0&1&-3&5\ |\ 0\\2&-4&4&-4\ |\ 0\end{array}\right]`

After this, we decrease this to reduce the formation of the row echelon

`R_3 = R_3 -2R_1 \rightarrow \left[\begin{array}{cccc}1&-3&5&-5\ |\ 0\\0&1&-3&5\ |\ 0\\0&2&-6&6\ |\ 0\end{array}\right]`

`R_3 = R_3 -2R_2 \rightarrow \left[\begin{array}{cccc}1&-3&5&-5\ |\ 0\\0&1&-3&5\ |\ 0\\0&0&0&-4\ |\ 0\end{array}\right]`

`R_2 = 4R_2 +5R_3 \rightarrow \left[\begin{array}{cccc}1&-3&5&-5\ |\ 0\\0&4&-12&0\ |\ 0\\0&0&0&-4\ |\ 0\end{array}\right]`

`R_2 = (R_2)/(4), R_3 = (R_3)/(-4) \rightarrow \left[\begin{array}{cccc}1&-3&5&-5\ |\ 0\\0&1&-3&0\ |\ 0\\0&0&0&1\ |\ 0\end{array}\right]`

`R_1 = R_1 +3 R_2 \rightarrow \left[\begin{array}{cccc}1&0&-4&-5\ |\ 0\\0&1&-3&0\ |\ 0\\0&0&0&-1\ |\ 0\end{array}\right]`

`R_1 = R_1 +5 R_3 \rightarrow \left[\begin{array}{cccc}1&0&-4&0\ |\ 0\\0&1&-3&0\ |\ 0\\0&0&0&-1\ |\ 0\end{array}\right]`

`= x_1 - 4x_3 = 0\\\\x_1 = 4x_3\\\\x_2 - 3x_3 = 0\\\\ x_2 = 3x_3\\\\x_4 = 0`

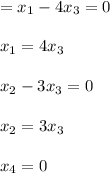
`x = \left[\begin{array}{c}4x_3&3x_3&x_3\\0\end{array}\right] \\\\ x_3 = \left[\begin{array}{c}4&3&1\\0\end{array}\right]`

By applying the above matrix, we can easily reach an answer