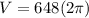Answer:

Explanation:
Given that :
Find the volume of the region enclosed by the cylinder
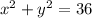 and the plane z = 0 and y + z = 36
and the plane z = 0 and y + z = 36
From y + z = 36
z = 36 - y
The volume of the region can be represented by the equation:

In this case;
D is the region given by

Relating this to polar coordinates
x = rcosθ y = rsinθ
x² + y² = r²
x² + y² = 36
r² = 36
r =

r = 6
dA = rdrdθ
r → 0 to 6
θ to 0 to 2π
Therefore:

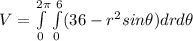
![V = \int\limits^(2 \pi) _0 [(36r^2)/(2)- (r^3)/(3)sin \theta]^6_0 \ d\theta](https://img.qammunity.org/2021/formulas/mathematics/college/1m3kvmwwi7c18bivr51h2l5rzp35ztltre.png)
![V = \int\limits^(2 \pi) _0 [648- (216)/(3)sin \theta]d\theta](https://img.qammunity.org/2021/formulas/mathematics/college/tu8elmd8guqyzgydkimh2yu7pgd5w8tiby.png)
![V = \int\limits^(2 \pi) _0 [648+(216)/(3)cos \theta]d\theta](https://img.qammunity.org/2021/formulas/mathematics/college/8z42r95qrjyou8ax73bp0f2i7l6dtqoza2.png)
![V = [648+(216)/(3)cos \theta]^(2 \pi)_0](https://img.qammunity.org/2021/formulas/mathematics/college/62jeocturagmleemszdl0c4eesoqypxz55.png)
![V = [648(2 \pi -0)+(216)/(3)(1-1)]](https://img.qammunity.org/2021/formulas/mathematics/college/heqn7wt58jkg55r03bwcdvv5t9wsqwua8a.png)
![V = [648(2 \pi )+(216)/(3)(0)]](https://img.qammunity.org/2021/formulas/mathematics/college/6xouh1xx5caa3o8pp8zknzxv1qjkm99o6u.png)