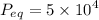Question

Determine a differential equation that models the growth of a population of fish as a function of time in days under each of the following hypotheses:

a) The rate of population increase is proportional to the size of the population. The population increases by 2 percent per day. (Treat time in days as a continuous variable, i.e. the rate at which the population increases is .02 times the population size.) dP/dt =
b) The rate of population increase is again proportional to the size of the population with the same constant of proportionality but 4 percent of the population is harvested each day. dP/dt =
c) The rate of population increase is again proportional to the size of the population with the same constant of proportionality but 1000 fish are harvested each day. dP/dt =
d) The equation in part c) has a threshhold. What is it?

Answer 1

Explanation:

a).

It is given that rate at which the population increases is directly proportional to size of the population. Thus we have,

`(dP)/(dt)\propto P`

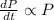
It is given in the question that the population increases by 2% in one day. Now we know that the time in days is a continuous variable, so we have

2% of P =
`$(2)/(100)* P$`

`$\therefore (dP)/(dt)=0.02 P $`

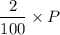
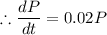
b).

It is given that the population is harvested by 4 % in one day

`$\therefore (dP)/(dt) =0.02P-0.04P$`

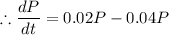
(Since 4% of the P is harvested.)

`$\therefore (dP)/(dt)=-0.02P$`

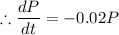
c).

It is given that 1000 fish are being harvested or removed in one day.

`$\therefore (dP)/(dt)= 0.02 P-1000$`

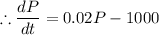
d).

The threshold is given by

`$0.02 P_(eq)-1000=0$`

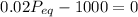
`$\therefore P_(eq)=(1000)/(0.02)$`

or
`$P_(eq)=5* 10^4$`