Question

SOMEONE PLEASE HELP ME!!! I REALLY NEED SOME HELP!!!

Which of the following points is a solution of the inequality y < - lxl?

A. (1, -2)
B. (1, -1)
C. (1, 0)​

Answer 1

A. (1, -2)

Explanation:

We can substitute the variables of x and y into the inequality of
`y < -|x|`.

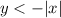Let's start with A, -2 being y and 1 being x.

`-2 < - |1|`

The absolute value of 1 is 1, and negating that gets us -1.

`-2 < -1`

Indeed, -2 is less than -1! So A is a solution to the inequality.

Let's test the rest of them, just in case.

For B:

`-1 < -|1|`

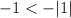
Absolute value of 1 is 1, negating it is -1.

`-1<-1`

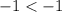
-1 is EQUAL to -1, not less than it, so is not a solution to the inequality.

Let's try C.

`0 < -|1|`

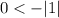
Absolute value of 1 is 1, negating it is -1.

`0 < -1`

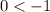
0 is GREATER than -1, so that is not a solution to the inequality.

Hope this helped!