Question

Triangle ABC is rotated about the origin by 270° to form the triangle A′B′C′, then translated upward 10 units to form triangle A″B″C″. Which of the following statements is true for ΔABC and ΔA″B″C″? A)There isn't enough information to identify whether ΔABC and ΔA″B″C″ are congruent or similar. B)ΔABC and ΔA″B″C″ are neither similar nor congruent. C)ΔABC and ΔA″B″C″ are similar triangles. D)ΔABC and ΔA″B″C″ are congruent triangles.

Answer 1

Answer:A-B

Explanation:

Answer 2

The correct answer is option:

D) ΔABC and ΔA″B″C″ are congruent triangles.

Explanation:

Given

1. ΔABC is first rotated about the origin by 270° to form the triangle A′B′C′.
2. 
   `\triangle A'B'C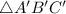'` is then translated upwards 10 units to form
   `\triangle A''B''C''`

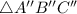
To find: The true statement among the given options.

Solution:

Let the triangle be situated in 1st quadrant.

It is rotated about the origin by
`270^\circ`.

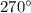Now, it moves towards quadrant 2 if it is rotated clockwise. It is termed as

`\triangle A'B'C'`.

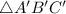It is given that now it is translated 10 units upwards. i.e. 10 units added to x coordinate of each vertex to form
`\triangle A''B''C''`.

Now, we can see that there is no change in the dimensions of the triangle. We are just changing the location of the triangle.

So, all its angles will be equal to each other and all the sides will be equal to each other.

i.e.

`\angle A = \angle A''\\\angle B = \angle B''\\\angle C = \angle C''\\Side\ AB = Side\ A''B''\\Side\ BC = Side\ B''C''\\Side\ AC = Side\ A''C''`

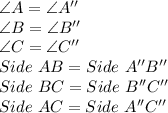
Hence, the correct option is:

D)ΔABC and ΔA″B″C″ are congruent triangles.