Answer:
Explained below.
Explanation:
X = annual consumption in the United States in 2008 of HFCS
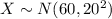
(a)
Find the probability a randomly selected American consumes more than 50 lbs of HFCS per year.
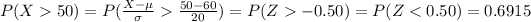
P (X > 50) = 0.6915.
(b)
Find the probability a randomly selected American consumes between 30 and 90 lbs of HFCS per year.

P (30 < X < 90) = 0.8664.
(c)
Find the 80th percentile of annual consumption of HFCS.
P (X < x) = 0.80
⇒ P (Z < z) = 0.80
⇒ z = 0.84
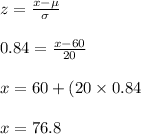
80th percentile = 76.8.
(d)
In a sample of 40 Americans how many would you expect to consume more than 50 pounds of HFCS per year.
P (X > 50) = 0.6915
Number of American who consume more than 50 lbs = 40 × 0.6915
= 27.66
≈ 28
Expected number = 28.
(e)
Between what two numbers would you expect to contain 95% of Americans HFCS annual consumption?
According to the Empirical rule, 95% of the normally distributed data lies within 2 standard deviations of mean.

Range = 20 < X < 100.
(f)
Find the quartile and Interquartile range for this population.
1st quartile: Q₁
P (X < Q₁) = 0.25
⇒ P (Z < z) = 0.25
⇒ z = -0.67
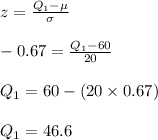
3rd quartile: Q₃
P (X < Q₃) = 0.75
⇒ P (Z < z) = 0.75
⇒ z = 0.67
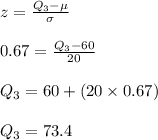
Inter quartile range:
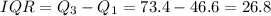
(g)
Compute the z-score for x = 105 lbs as follows:

Z-scores greater than +2.00 or less than -2.00 are considered as unusual.
Thus, the result unusual.