Question

Given: XY - tangent to circles k1(P) and k2(O) OX=16, PY=6 and OP=26 Find: XY

Answer 1

the answer is XY = 24 units.

Explanation:

Given:

XY is tangent to the circles with center P and O respectively.

OX=16 units

PY=6 units

OP=26 units

To find:

Side XY = ?

Solution:

As per given statement, the diagram of two circles and their tangent is shown in the diagram.

We need to do one construction here,

Draw a line parallel to tangent XY from P towards OX such that it meets OX at A .

Now, let us consider triangle
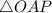`\triangle OAP`. It is a right angled triangle.

With sides Hypotenuse, OP = 26 units

Perpendicular, OA = 16 -6 = 10 units

Base AP is equal to XY.

If we find the value of Base AP, the value of XY is calculated automatically.

Let us use pythagorean theorem in
`\triangle OAP`:

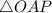According to pythagorean theorem:

`\text{Hypotenuse}^(2) = \text{Base}^(2) + \text{Perpendicular}^(2)\\\Rightarrow OP^(2) = AP^(2) + OA^(2) \\\Rightarrow 26^2=XY^2+10^2\\\Rightarrow XY^2 = 676- 100\\\Rightarrow XY = √(576)\\\Rightarrow XY = 24\ units`

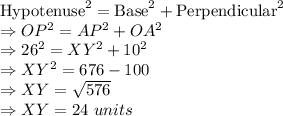
Hence, the answer is XY = 24 units.