Question

The graph below represents which systems of inequalities?

A. Y> 2x+3
y>+3
B. Y<2x+3
y C. Y<3x+2
y<-x+2
D Y> - 2x+ 3
y>x+3

Answer 1

y ≤ x + 3

y ≤ -2x + 3

Explanation:

Graph attached shows two solid lines having equal y-intercepts as 3 units.

Since one line passes through two points (0, 3) and (-3, 0),

Slope of this line 'm' =
`(y_2-y_1)/(x_2-x_1)`

=
`(3-0)/(0+3)`

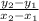
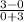
= 1

Let the equation of the this line is,

y = mx + b

where m = slope of the line

b = y-intercept

Therefore, equation of the line having slope = 1 and y-intercept = 3 units,

y = 1.x + 3

y = x + 3

Since, shaded region shown is on the left of the line y = x + 3

Therefore, y ≤ x + 3 will be the inequality with shaded area in green.

Slope of the second line passing through (0, 3) and (1.5, 0)

m' =
`(3-0)/(0-1.5)`

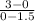
= -2

Therefore, equation of the second line will be,

y = (-2)x + 3

y = -2x + 3

Since shade area (In yellow) is below the given solid line, equation of the inequality will be,

y ≤ -2x + 3