Question

In a Gallup poll of randomly selected adults, 66% said that they worry about identity theft. For a group of 1013 adults, the mean of those who do not worry about identify theft is closest to:

Answer 1

`Mean = 344`

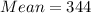
Explanation:

Given

`Population = 1013`

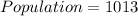
Let p represents the proportion of those who worry about identity theft;

`p = 66\%`

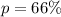
Required

Mean of those who do not worry about identity theft

First, the proportion of those who do not worry, has to be calculated;

Represent this with q

In probability;

`p + q = 1`

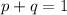
Make q the subject of formula

`q = 1 - p`

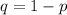
Substitute
`p = 66\%`

`q = 1 - 66\%`

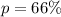
Convert percentage to fraction

`q = 1 - 0.66`

`q = 0.34`

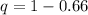
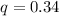
Now, the mean can be calculated using:

`Mean = nq`

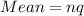
Where n represents the population

`Mean = 1013 * 0.34`

`Mean = 344.42`

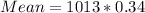
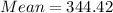
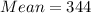`Mean = 344` (Approximated)