Question

You are flying a hang glider at 14 mph in the northeast direction (45°). The wind is blowing at 4 mph from due north.

a) What is your airspeed?
b) What angle (direction) are you flying?
c) The wind increases to 14 mph from the north. Now what is your airspeed and what direction are you flying? If your destination is to the northeast, how would you change your speed or direction so you might make it there?

Answer 1

a) 17.05 mph

b) 54.7° northeast direction

c) 10.71 mph

The direction is -22.58° relative to the east.

To head northeast, you must either increase your gliding speed or increase your angle relative to the x-axis greater than 45°.

Step-by-step explanation:

The question is a little confusing but, I guess the correct question should be;

You are flying a hang glider at 14 mph in the northeast direction (45°). The wind is blowing at 4 mph due north.

a) What is your airspeed?

b) What angle (direction) are you flying?

c) The wind increases to 14 mph from north. Now what is your airspeed and what direction are you flying? If your destination is to the northeast, how would you change your speed or direction so you might make it there?

NB: The difference in the question and my suggestion is highlighted boldly.

Your speed = 14 mph

direction is 45° northeast

Th wind speed = 4 mph

direction is north

We resolve the your speed and the wind speed into the horizontal and vertical components

For vertical the component component

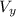`V_(y)` = 14(sin 45) + 4 = 9.89 + 4 = 13.89 mph

For the horizontal speed component

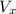`V_(x)` = 14(cos 45) + 0 = 9.89 + 0 = 9.89 mph

Resultant speed =
`\sqrt{V^(2) _(y)+V^(2) _(x) }`

==>
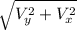
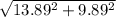`\sqrt{13.89^(2) +9.89^(2) }` = 17.05 mph This is your airspeed

b) To get your direction, we use

tan ∅ =
`V_(y)` /
`V_(x)`

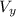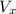
tan ∅ = 13.89/9.89 = 1.413

∅ =
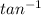`tan^(-1)`(1.413) = 54.7° northeast direction

c) If the wind increases to 14 mph from the north, then it means the wind blows due south. As before, only the vertical component is affected .

In this case,

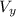`V_(y)` = 14(sin 45) - 14 = 9.89 - 14 = -4.11 mph

Resultant speed =
`\sqrt{V^(2) _(y)+V^(2) _(x) }`

==>
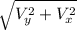
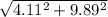`\sqrt{4.11^(2) +9.89^(2) }` = 10.71 mph This is your airspeed

Your direction will be,

tan ∅ =
`V_(y)` /
`V_(x)`

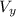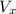
tan ∅ = -4.11/9.89 = -0.416

∅ =
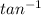`tan^(-1)`(-0.416) = -22.58° this is the angle you'll travel relative to the east.

To head northeast, you must either increase your gliding speed or increase your angle relative to the x-axis greater than 45°.