Question

Losses covered by a flood insurance policy are uniformly distributed on the interval (0,2). The insurer pays the amount of the loss in excess of a deductible d. The probability that the insurer pays at least 1.20 on a random loss is 0.30. Calculate the probability that the insurer pays at least 1.44 on a random loss.

Answer 1

The probability that the insurer pays at least 1.44 on a random loss is 0.18.

Explanation:

Let the random variable X represent the losses covered by a flood insurance policy.

The random variable X follows a Uniform distribution with parameters a = 0 and b = 2.

The probability density function of X is:

`f_(X)(x)=(1)/(b-a);\ a<X<b\\\\\Rightarrow f_(X)(x)=(1)/(2)`

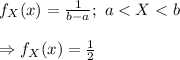
It is provided, the probability that the insurer pays at least 1.20 on a random loss is 0.30.

That is:

`P(X\geq 1.2+d)=0.30\\`

⇒

`P(X\geq 1.2+d)=\int\limits^(2)_(1.2+d){(1)/(2)}\, dx`

`0.30=(2-1.2-d)/(2)\\\\0.60=0.80-d\\\\d=0.80-0.60\\\\d=0.20`

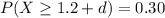
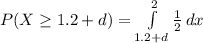
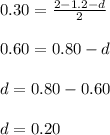
The deductible d is 0.20.

Compute the probability that the insurer pays at least 1.44 on a random loss as follows:

`P(X\geq 1.44+d)=P(X\geq 1.64)`

`=\int\limits^(2)_(1.64){(1)/(2)}\, dx\\\\=|(x)/(2)|\limits^(2)_(1.64)\\\\=(2-1.64)/(2)\\\\=0.18`

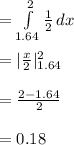
Thus, the probability that the insurer pays at least 1.44 on a random loss is 0.18.