Answer:
The error that might occur is
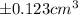
Explanation:
Given
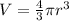
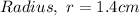
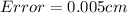
Required
Determine the error that might occur in the volume of the tumor
Given that there's an error in measurement, this question will be solved using the concept of differentiation;
First, we'll rewrite the given parameters in differentiation notations;
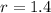 --- Radius
--- Radius
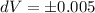 --- Change in measurement
--- Change in measurement
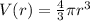 --- Volume as a function of radius
--- Volume as a function of radius
The relationship between the above parameters is as follows;

This can be rewritten as
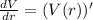
Substitute
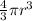 for
for

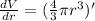
Multiply both sides by dr
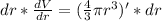

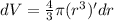
Differentiate
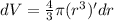
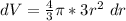
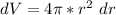
Substitute the values of r, dr and take
 as 3.142
as 3.142
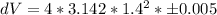
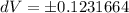
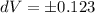 (Approximated)
(Approximated)
Hence, the error that might occur is ±0.123