Question

Describe the transformation of ƒ(x) = 10x which is given by g(x) = 103x. Question 20 options: A) g(x) is shrunk horizontally by a factor of 1∕3 compared to ƒ(x). B) g(x) is stretched vertically by a factor of 3 compared to ƒ(x). C) g(x) is shrunk vertically by a factor of 1∕3 compared to ƒ(x). D) g(x) is stretched horizontally by a factor of 3 compared to ƒ(x).

Answer 1

Explanation:

Answer: A) g(x) is shrunk horizontally by a factor of 1∕3 compared to ƒ(x).

Answer 2

Answer: A) g(x) is shrunk horizontally by a factor of 1∕3 compared to ƒ(x).

Explanation:

Given: f(x) 10x

g(x) =10(3x)

= f(3x)

Since, f(ax) is a horizontal compression when a> 1 by the factor of
`(1)/(a).`

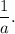
That means g(x) is shrunk horizontally by a factor of
`(1)/(3)` compared to ƒ(x).

So, the correct option is A) g(x) is shrunk horizontally by a factor of 1∕3 compared to ƒ(x).