Answers: x = -11 and x = 3
======================================================
Step-by-step explanation:
There are at least three ways to solve this.
----------------------------------------------
Method 1:
We could graph y = (x-2)(x+10) using a tool like Desmos. Graph y = 13 as well which is a horizontal line.
Check out the screenshot shown below.
The parabola in red and the horizontal line in blue intersect at the locations (-11, 13) and (3, 13)
We only focus on the x coordinates of the intersection points.
Therefore, the two solutions are x = -11 and x = 3
The order of the solutions doesn't matter.
----------------------------------------------
Method 2:
Expand things out and get everything to one side
(x-2)(x+10) = 13
x^2 + 10x - 2x - 20 = 13
x^2 + 8x - 20 - 13 = 0
x^2 + 8x - 33 = 0
From here we can use the quadratic formula
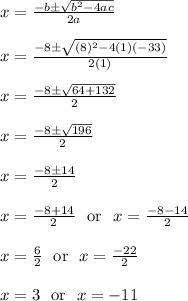
----------------------------------------------
Method 3:
Instead of using the quadratic formula, we could factor.
To factor x^2+8x-33, we need to find two numbers that
Through trial and error, you should get 11 and -3
- 11 times -3 = -33
- 11 plus -3 = 8
So,
x^2+8x-33 = 0
(x+11)(x-3) = 0
x+11 = 0 or x-3 = 0
x = -11 or x = 3