Question

Describe the transformation of ƒ(x) = log5 x which is given by g(x) = 3 log5 (x−7). Question 16 options: A) g(x) is shrunk vertically by a factor of 1∕3 and translated to the right 7 units compared to ƒ(x). B) g(x) is stretched vertically by a factor of 2 and translated to the left 7 units compared to ƒ(x). C) g(x) is stretched vertically by a factor of 3 and translated to the right 7 units compared to ƒ(x). D) g(x) is shrunk vertically by a factor of 1∕3 and translated to the left 7 units compared to ƒ(x)

Answer 1

C) g(x) is stretched vertically by a factor of 3 and translated to the right 7 units compared to ƒ(x).

Explanation:

Notice that by transforming
`f(x)=log_5\,(x)` into
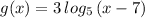`g(x)=3\,log_5\,(x-7)` we have performed the following transformations:

a) a horizontal shift to the right 7 units by subtracting 7 from the x-variable, and

b) stretching the full function vertically by a factor of 3, by multiplying the full function by 3.

Therefore, our answer matches answer C in the list of possible options