Answer:
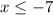
The graph has a closed circle.
–7 is part of the solution.
Explanation:
Given
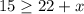
Required
Select 3 options from the given list of options
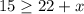
Subtract 22 from both sides
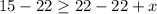

Swap positions of the expression; Note that the inequality sign will change
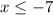
This means x less-than-or-equal-to negative 7
There are two options left to select;
The inequality sign in
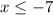 implies that the graph has a close circle.
implies that the graph has a close circle.
Inequality signs such as
 and
and
 signifies a close circle
signifies a close circle
There is only one option left to select;
Lastly;
Split the expression
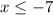 into two
into two
We have:
 or
or
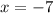
Because
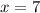 ,
,
Then, -7 is also a part of the solution