Question

The mean height of a Clydesdale horse is 72 inches with a standard deviation of 1.2 inches. What is the probability that a Clydesdale is greater than 75 inches tall?

Answer 1

0.0062

Explanation:

Given that:

Mean (μ) = 72 inches, Standard deviation (σ) = 1.2 inches.

The z score is a measure in statistics is used to determine by how many standard deviation the raw score is above or below the mean. If the raw score is above the mean, the z score is positive and if the raw score is below the mean, the z score is negative.

The z score is given as:

`z=(x-\mu)/(\sigma)`

For Clydesdale is greater than 75 inches tall, x = 75 inches, the z score is:

`z=(x-\mu)/(\sigma)=(75-72)/(1.2) =2.5`

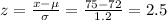
The probability that a Clydesdale is greater than 75 inches tall = P(X > 75) = P(Z > 2.5) = 1 - P(Z < 2.5) = 1 - 0.9938 = 0.0062 = 0.62%

The probability that a Clydesdale is greater than 75 inches tall is 0.62%