Answer:
6.34 seconds.
Explanation:
The object will hit the ground when h = 0.
-16t^2 + 90t + 72 = 0
8t^2 - 45t - 36 = 0
We can then use the quadratic formula to solve.
[please ignore the A-hat; that is a bug]

=

=
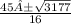
=

(45 - 56.36488268) / 16 = -0.7103051678
(45 + 56.36488268) / 16 = 6.335305168
Since the time cannot be negative, the object will hit the ground after about 6.34 seconds.
Hope this helps!