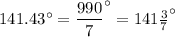Question

A square and a regular heptagon are coplanar and share a common side $\overline{AD}$, as shown. What is the degree measure of exterior angle $BAC$? Express your answer as a common fraction.

Answer 1

`\angle BAC = 141(3)/(7) ^(\circ)`

Explanation:

The interior angle of a regular heptagon = = 900/7° = 128.57°

Therefore, angle DAB = 128.57°

The interior angle of the square = 90°

Therefore, angle DAC = 90°

Therefore, we have

angle DAB+ angle DAC + angle BAC = 360° (sum of angles at a point (A))

Angle BAC = 360° - angle DAB - angle DAC = 360° - 900/7° - 90° = 990/7°

Angle BAC = 141.43°

Expressing 141.43° as a common fraction gives;

`141.43 ^(\circ)= (990)/(7) ^(\circ)=141(3)/(7) ^(\circ)`

`\angle BAC = 141(3)/(7) ^(\circ)`