Question

Statistics question; please help.

Scott has hired you to check his machine prior to starting an order. To check it, you set the machine to create 1.5 inch screws and manufacture a random sample of 200 screws. That sample of screws has an average length of 1.476 inches with a standard deviation of 0.203 inches.

Does this sample provide convincing evidence that the machine is working properly?
Thank you in advance!

Answer 1

Does this sample provide convincing evidence that the machine is working properly?

Yes.

Explanation:

Normal distribution test:

`$z=(x- \mu )/( (\sigma)/(√(n)) )=( (x-\mu)√(n))/(\sigma) $`

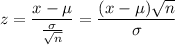
Where,

`x: \text{ sample mean}`

`\sigma: \text{ standard deviation}`

`n: \text{ sample size determination}`

`\mu: \text{ hypothesized size of the screw}`

`$z=((1.476-1.5)√(200) )/(0.203 ) $`

`$z=((-0.024)10√(2) )/(0.203 ) $`

`z \approx -1.672`

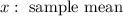
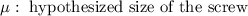
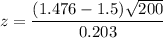
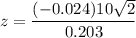
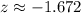
Once the significance level was not given, It is usually taken an assumption of a 5% significance level.

Taking the significance level of 5%, which means a confidence level of 95%, we have a z-value of
`\pm 1.96`

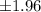
Therefore, we fail to reject the null. It means that the hypothesis test is not statistically significant: the average length is not different from 1.5!