Answer:
1)
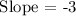
2)
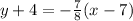
3)
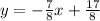
Explanation:
We want to write the equation of the line that passes through the points (7, -4) and (-1, 3) first in point-slope form and then in slope-intercept form.
1)
First and foremost, we will need to find the slope of the line. So, we can use the slope-formula:

Let (7, -4) be (x₁, y₁) and let (-1, 3) be (x₂, y₂). Substitute them into our slope formula. This yields:
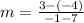
Subtract. So, our slope is:
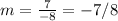
2)
Now, let's use the point-slope form:

We will substitute -7/8 for our slope m. We will also use the point (7, -4) and this will be our (x₁, y₁). So, substituting these values yield:
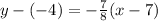
Simplify. So, our point-slope equation is:
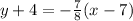
3)
Finally, we want to convert this into slope-intercept form. So, let's solve for our y.
On the right, distribute:
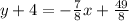
Subtract 4 from both sides. Note that we can write 4 using a common denominator of 8, so 4 is 32/8. This yields:
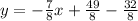
Subtract. So, our slope-intercept equation is:
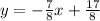
And we're done!