Answer:
I = E/R e^{-t/RC}
Step-by-step explanation:
In a capacitor charging circuit you must have a DC power source, the capacitor, a resistor, and a switch. When closing the circuit,
E -q / c-IR = 0
we replace the current by its expression and divide by the resistance
I = dq / dt
dq / dt = E / R -q / RC
dq / dt = (CE -q) / RC
we solve the equation
dq / (Ce-q) = -dt / RC
we integrate and evaluate for the charge between 0 and q and for the time 0 and t
ln (q-CE / -CE) = -1 /RC (t -0)
eliminate the logarithm
q - CE = CE
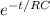
q = CE (1 + 1/RC e^{-t/RC} )
In general the teams measure the current therefore we take the derivative to find the current
i = CE (e^{-t/RC} / RC)
I = E/R e^{-t/RC}
This expression is the one that describes the charge of a condensate in a DC circuit