Question

The speed of a particle moving in a circle 2.0 m in radius increases at the constant rate of 4.4 m/s2. At an instant when the magnitude of the total acceleration is 6.0 m/s2, what is the speed of the particle? Group of answer choices

Answer 1

The speed of the particle is 2.86 m/s

Step-by-step explanation:

Given;

radius of the circular path, r = 2.0 m

tangential acceleration,
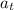`a_t` = 4.4 m/s²

total magnitude of the acceleration, a = 6.0 m/s²

Total acceleration is the vector sum of tangential acceleration and radial acceleration

`a = √(a_c^2 + a_t^2)\\\\`

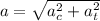
where;

`a_c` is the radial acceleration

`a = √(a_c^2 + a_t^2)\\\\a^2 = a_c^2 + a_t^2\\\\a_c^2 = a^2 -a_t^2\\\\a_c = √(a^2 -a_t^2)\\\\a_c = √(6.0^2 -4.4^2)\\\\a_c = √(16.64)\\\\a_c = 4.08 \ m/s^2`

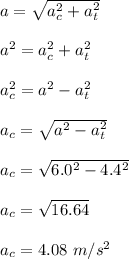
The radial acceleration relates to speed of particle in the following equations;

`a_c = (v^2)/(r)`

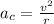
where;

v is the speed of the particle

`v^2 = a_c r\\\\v= √(a_c r) \\\\v = √(4.08 *2)\\\\v = 2.86 \ m/s`

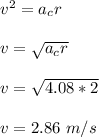
Therefore, the speed of the particle is 2.86 m/s