Question

Suppose taxi fares from Logan Airport to downtown Boston is known to be normally distributed and a sample of seven taxi fares produces a mean fare of $21.51 and a 95% confidence interval of [$20.52, $22.48]. Which of the following statements is a valid interpretation of the confidence interval?

a. 95% of all taxi fares are between $20.52 and $22.48.
b. We are 95% confident that a randomly selected taxi fare will be between $20.52 and $22.48.
c. We can report that the average taxi fare between Logan Airport and downtown Boston will fall between $20.52 and $22.48.
d. With 95% confidence

Answer 1

The correct option is C

Explanation:

From the question we are told that

The sample mean is
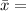`\= x =`$21.51

The 95% confidence level interval is [$ 20.52 , $22.48]

Generally the 95% confidence level interval is mathematically represented as

`\= x - MOE < \mu < \= x + MOE`

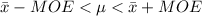
Where MOE is the margin of error which defines in percentage the amount by which the sample mean taxi fare(for the 7 taxi ) will differ from the average taxi fare between Logan Airport and downtown Boston will fall between

Also
`\mu` is the average taxi fare between Logan Airport and downtown Boston

So we see that the this 95% confidence level interval tells us that the average taxi fare between Logan Airport and downtown Boston will fall between $20.52 and $22.48.