Question

A typing instructor builds a regression model to investigate what factors determine typing speed for students with two months of instruction. Her regression equation looks like: Y' = 11 + 7x1 + 5x2 + 3x3 where: Y' = typing speed in words per minute; x1= hours of instruction per week; x2= hours of practice per week; x3 = hours of typing per week necessary for school or work;

Answer 1

The range that has a 95.45% probability that that student's typing speed will be in two months is [49.5, 65.5].

Step-by-step explanation:

The compete question is:

A new student is taking 2 hrs of typing instruction per week, will practice 5 hrs per week and must type 2.5 hours per week for work. If the standard error of the estimate is 4, within what range do we have a 95.45% probability that that student's typing speed will be in two months?

Solution:

The regression equation formed by the typing instructor to investigate what factors determine typing speed for students with two months of instruction is as follows:

`Y' = 11 + 7x_(1) + 5x_(2) + 3x_(3)`

Here,

Y' = typing speed in words per minute

x₁ = hours of instruction per week

x₂ = hours of practice per week

x₃ = hours of typing per week necessary for school or work

Compute the value of Y' for the given values of x₁, x₂ and x₃ as follows:

`Y' = 11 + 7x_(1) + 5x_(2) + 3x_(3)`

`=11+(7* 2)+(5* 5)+(3* 2.5)\\=11+14+25+7.5\\=57.5`

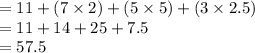
So, the typing speed of this student in words per minute is 57.5.

The range providing the (1 - α)% prediction interval for values of Y' is:

`Y=[Y'\pm t_(\alpha/2, (n-2))* SE]`

Since the data selected is for 2 months the sample size is too large.

The critical value of t is 2.

Compute the range as follows:

`Y=[Y'\pm t_(\alpha/2, (n-2))* SE]`

`=[57.5\pm 2* 4]\\\\=[57.5\pm 8]\\\\=[49.5, 65.5]`

Thus, the range that has a 95.45% probability that that student's typing speed will be in two months is [49.5, 65.5].