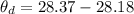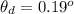Question

The refractive index n of transparent acrylic plastic (full name Poly(methyl methacrylate)) depends on the color (wavelength) of the light passing through it. At wavelength 486.1 nm (blue, designated with letter F) -> nF=1.497, and at wavelength 656.3 nm (red, designated with letter C) -> nC=1.488. Two beams (one of each wavelength) are prepared to coincide, and enter the flat polished surface of an acrylic block at angle of 45 arc degree measured from the normal to the surface. What is the angle between the blue beam and the red beam in the acrylic block?

Answer 1

The angle between the blue beam and the red beam in the acrylic block is

`\theta _d =0.19 ^o`

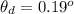
Step-by-step explanation:

From the question we are told that

The refractive index of the transparent acrylic plastic for blue light is
`n_F = 1.497`

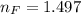
The wavelength of the blue light is
`F = 486.1 nm = 486.1 *10^(-9) \ m`

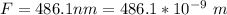
The refractive index of the transparent acrylic plastic for red light is
`n_C = 1.488`

The wavelength of the red light is
`C = 656.3 nm = 656.3 *10^(-9) \ m`

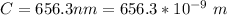
The incidence angle is
`i = 45^o`

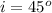
Generally from Snell's law the angle of refraction of the blue light in the acrylic block is mathematically represented as

`r_F = sin ^(-1)[(sin(i) * n_a )/(n_F) ]`

Where
`n_a` is the refractive index of air which have a value of
`n_a = 1`

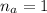
So

`r_F = sin ^(-1)[(sin(45) * 1 )/( 1.497) ]`

`r_F = 28.18^o`

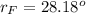
Generally from Snell's law the angle of refraction of the red light in the acrylic block is mathematically represented as

`r_C = sin ^(-1)[(sin(i) * n_a )/(n_C) ]`

Where
`n_a` is the refractive index of air which have a value of
`n_a = 1`

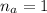
So

`r_C = sin ^(-1)[(sin(45) * 1 )/( 1.488) ]`

`r_F = 28.37^o`

The angle between the blue beam and the red beam in the acrylic block

`\theta _d = r_C - r_F`

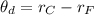
substituting values

`\theta _d = 28.37 - 28.18`

`\theta _d =0.19 ^o`