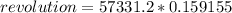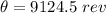Answer:
a
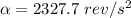
b
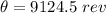
Step-by-step explanation:
From the question we are told that
The maximum angular speed is
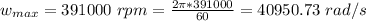
The time taken is
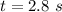
The minimum angular speed is
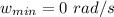 this is because it started from rest
this is because it started from rest
Apply the first equation of motion to solve for acceleration we have that
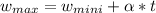
=>
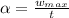
substituting values

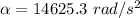
converting to
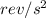
We have
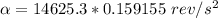
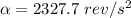
According to the first equation of motion the angular displacement is mathematically represented as
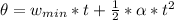
substituting values
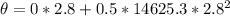
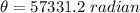
converting to revolutions