Question

Use I=∫r2 dm to calculate I of a slender uniform rod of length L, about an axis at one end perpendicular to the rod. note: a "slender rod" often refers to a rod of neglible cross sectional area, so that the volume is the Length, and the mass density X Length.

Answer 1

The moment of inertia of a slender uniform rod of length L about an axis at one end perpendicular to the rod is
`I = (1)/(3)\cdot m \cdot L^(2)`.

Step-by-step explanation:

Let be an uniform rod of length L whose origin is located at one one end and axis is perpendicular to the rod, such that:

`\lambda = (dm)/(dr)`

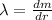
Where:

`\lambda` - Linear density, measured in kilograms per meter.

`m` - Mass of the rod, measured in kilograms.

`r` - Distance of a point of the rod with respect to origin.

Mass differential can translated as:

`dm = \lambda \cdot dr`

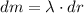
The equation of the moment of inertia is represented by the integral below:

`I = \int\limits^(L)_(0) {r^(2)} \, dm`

`I = \lambda \int\limits^(L)_(0) {r^(2)} \, dr`

`I = \lambda \cdot \left((1)/(3)\cdot L^(3) \right)`

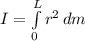
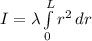
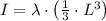
`I = (1)/(3)\cdot m \cdot L^(2)` (as
`m = \lambda \cdot L`)

The moment of inertia of a slender uniform rod of length L about an axis at one end perpendicular to the rod is
`I = (1)/(3)\cdot m \cdot L^(2)`.