Answer:
The correct option is;
![h(x) = \sqrt[3]{x + 2}](https://img.qammunity.org/2021/formulas/mathematics/high-school/npmo6rzp7rv7824w7iil8jwapja98bjto0.png)
Explanation:
Given that h(x) is a translation of f(x) = ∛x
From the points on the graph, given that the function goes through (-1, 1) and (-3, -1) we have;
When x = -1, h(x) = 1
When x = -3, h(x) = -1
h''(x) = (-2, 0)
Which gives
d²(∛(x + a))/dx²=
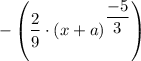 , have coordinates (-2, 0)
, have coordinates (-2, 0)
When h(x) = 0, x = -2 which gives;
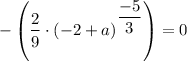
Therefore, a = (0/(-2/9))^(-3/5) + 2
a = 2
The translation is h(x) =
![\sqrt[3]{x + 2}](https://img.qammunity.org/2021/formulas/mathematics/high-school/poyfwetua5644kl2i5hjsa6ydagvm2ggid.png)
We check, that when, x = -1, y = 1 which gives;
h(x) =
![\sqrt[3]{-1 + 2} = \sqrt[3]{1} = 1](https://img.qammunity.org/2021/formulas/mathematics/high-school/u8s4w8fo96261t3kuhdsrn3fd8bw9nlrrz.png) which satisfies the condition that h(x) passes through the point (-1, 1)
which satisfies the condition that h(x) passes through the point (-1, 1)
For the point (-3, -1), we have;
h(x) =
![\sqrt[3]{-3 + 2} = \sqrt[3]{-1} = -1](https://img.qammunity.org/2021/formulas/mathematics/high-school/sraoq20phyb605blr9xsatpf8xt192m7qf.png)
Therefore, the equation, h(x) =
![\sqrt[3]{x + 2}](https://img.qammunity.org/2021/formulas/mathematics/high-school/poyfwetua5644kl2i5hjsa6ydagvm2ggid.png) passes through the points (-1, 1) and (-3, -1) and has an inflection point at (-2, 0).
passes through the points (-1, 1) and (-3, -1) and has an inflection point at (-2, 0).