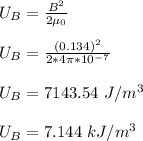Question

You would like to store 8.1 J of energy in the magnetic field of a solenoid. The solenoid has 620 circular turns of diameter 6.6 cm distributed uniformly along its 33 cm length.

A. How much current is needed?
_____________ A
B. What is the magnitude of the magnetic field inside the solenoid?
________________T
C. What is the energy density (energy/volume) inside the solenoid?
________________ kJ/m^3

Answer 1

(a) The current needed is 56.92 A

(b) The magnitude of the magnetic field inside the solenoid is 0.134 T

(c) The energy density inside the solenoid is 7.144 kJ/m³

Step-by-step explanation:

Given;

energy stored in the magnetic field of solenoid, E = 8.1 J

number of turns of the solenoid, N = 620 turns

diameter of the solenoid, D = 6.6 cm = 0.066 m

radius of the solenoid, r = D/2 = 0.033 m

length of the solenoid, L = 33 cm = 0.33 m

Inductance of the solenoid is given as;

`L= (\mu_o N^2 A)/(l)`

where;

A is the area of the solenoid = πr² = π (0.033)² = 0.00342 m²

μ₀ is permeability of free space = 4π x 10⁻⁷ H/m

`L= (4\pi*10^(-7) *620^2 *0.00342)/(0.33) \\\\L = 0.005 \ H`

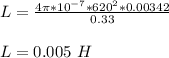
(A). How much current needed

Energy stored in magnetic field of solenoid is given as;

`E = (1)/(2) LI^2\\\\`

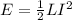
Where;

I is the current in the solenoid

`E = (1)/(2) LI^2\\\\I^2 = (2E)/(L)\\\\I = \sqrt{(2*8.1)/(0.005)}\\\\ I = 56.92 \ A`

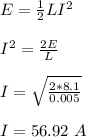
(B) The magnitude of the magnetic field inside the solenoid

B = μ₀nI

where;

n is number of turns per unit length

B = μ₀(N/L)I

B = (4π x 10⁻⁷)(620/0.33)(56.92)

B = 0.134 T

(C) The energy density (energy/volume) inside the solenoid

`U_B = (B^2)/(2\mu_0) \\\\U_B = ((0.134)^2)/(2*4\pi*10^(-7)) \\\\U_B = 7143.54 \ J/m^3\\\\U_B = 7.144 \ kJ/m^3`