Question

Solve the following system of equations

y = -x^2+3x+18
y = -2x+4

A.) (-7.8) and (2,10)
B.) (2,20) and (11,-18)
C.) (-2,8) and (7,-10)
D.) (-2,-20) and (-11,18)

Answer 1

The answer is option C

Explanation:

y = - x² + 3x + 18

y = - 2x + 4

Since they are both equal to y we equate them

That's,

- x² + 3x + 18 = - 2x + 4

x² - 5x - 14 = 0

Solve the quadratic equation

x² - 5x - 14 = 0

x² + 2x - 7x - 14 = 0

x(x + 2) - 7( x + 2) = 0

( x - 7)(x + 2) = 0

x - 7 = 0 x + 2 = 0

x = 7 x = - 2

Substitute the values of x into y = - 2x + 4

That's

when x = 7 when x = - 2

y = - 2(7) + 4 y = - 2(-2) + 4

y = - 14 + 4 y = 4 + 4

y = - 10 y = 8

So the solutions are

(7 , - 10) and ( - 2 , 8)

Hope this helps you

Answer 2

`\boxed{Option \ C}`

Explanation:

`y = -x^2+3x+18\\y = -2x+4`

Equating both equations

=>
`-x^2+3x+18 = -2x+4\\x^2-2x-3x+4-18 = 0\\x^2-5x-14=0`

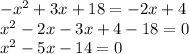
Using mid term break formula

=>
`x^2-7x+2x-14=0\\x(x-7)+2(x-7)=0\\Taking \ (x-7) \ common\\(x+2)(x-7) = 0`

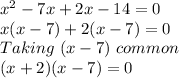
Either,

x + 2 = 0 OR x - 7 = 0

x = -2 OR x = 7

For, x = -2 , y is

=> y = -2x+4

=> y = -2(-2)+4

=> y = 4+4

=> y = 8

So, the ordered pair is (-2,8)

For x = 7 , y is

=> y = -2(7)+4

=> y = -14+4

=> y = -10

So, the ordered pair for this is (7, -10)

Solution Set = {(-2,8),(7,-10)}