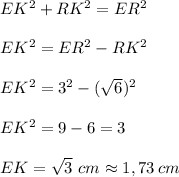Question

the length of each side of the ABCD EFGH cube is 6cm. If point P is located in the middle of line EH, point Q is in the middle of line EF, and point R is in the middle of line AE, determine the distance of point E to the PQR plane

Answer 1

The distance is:
`\sqrt3\ cm\approx1,73\,cm`

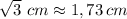
Explanation:

The distance of point E to the PQR plane it is the hight (vertical) of piramid PRQE

If point P is located in the middle of line EH, point Q is in the middle of line EF, and point R is in the middle of line AE than:

EP = EQ = ER = 0.5EF = 3 cm and m∠REQ = m∠QEP = m∠REP = 90° so triangles RQE, QPE and PRE are congruent.

RQ = QP = PR so triangle PQR is equilateral and from Pythagorean theorem (for ΔRQE):

`RQ^2=ER^2+EQ^2=3^2+3^2=2\cdot3^2\ \ \implies\ \ RQ=3\sqrt2`

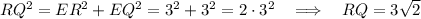
Then:
`RN=\frac{RQ\,\sqrt3}2`

and:
`RK=\frac23RN=\frac{RQ\,\sqrt3}3=\frac{3\sqrt2\cdot\,\sqrt3}3=\sqrt6`

Therefore from Pythagorean theorem (for ΔERK):

`EK^2+RK^2=ER^2\\\\EK^2=ER^2-RK^2\\\\EK^2=3^2-(\sqrt6)^2\\\\EK^2=9-6=3\\\\EK=\sqrt3\ cm\approx1,73\,cm`