Question

A parallelogram has side lengths of 13 and 17 and an

angle that measures 64º.
What is x, the length of the diagonal, to the nearest
whole number?

Answer 1

`x = 16`

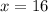
Explanation:

x = length of diagonal, can be calculated using the Law of Cosines as explained below:

a² = b² + c² - 2bc(cosA),

Where,

a = x

b = 17

c = 13

A = 64°

Plug in the values into the formula:

`x^2 = 17^2 + 13^2 - 2(17)(13)*cos(64)`

`x^2 = 289 + 169 - 442*0.4384`

`x^2 = 458 - 193.77`

`x^2 = 264.23`

`x = √(264.23)`

`x = 16.255`

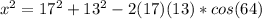
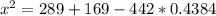
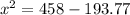
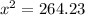
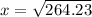
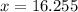
Length of diagonal,
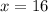`x = 16` (to nearest whole number)