Question

A garden has an area of 264ft^2. Its length is 10 ft more than its width. What are the dimensions of the​ garden?

Answer 1

Length = 22 ft

Width = 12 ft

Explanation:

Let length of the garden be ' x + 10 '

Let breath of the garden be ' x '

Area of the garden = 264 ft²

Now, let's find the breath of the garden 'x'

`x(x + 10) = 264`

Distribute X through the parentheses

`{x}^(2) + 10x = 264`

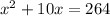
Move constant to left and change its sign

`{x}^(2) + 10x - 264 = 0`

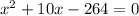
Write 10x as a difference

`{x}^(2) + 22x - 12x - 264 = 0`

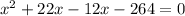
Factor out X from the expression

`x(x + 22) - 12x - 264 = 0`

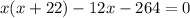
Factor out -12 from the expression

`x(x + 22) - 12(x + 22) = 0`

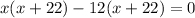
Factor out X +22 from the expression

`(x + 22)(x - 12) = 0`

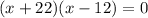
When the products of factors equals to 0 , at least one factor is 0

`x + 22 = 0`

`x - 12 = 0`

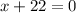
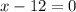
Solve for X

`x + 22 = 0`

`x = 0 - 22`

`x = - 22`

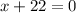
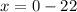
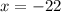
Again,

`x - 12 = 0`

`x = 0 + 12`

`x = 12`

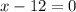
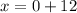
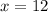
(The dimensions can't be negative. )

So, width = 12 ft

Now, let's find the length of the garden ' X + 10 '

`x + 10`

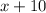
Plug the value of X

`12 + 10`

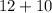
Calculate the sum

`= 22 \: ft`

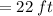
Therefore,

Length = 22 ft

Width = 12 ft

Hope this helps..

Best regards!