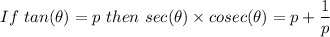Answer:
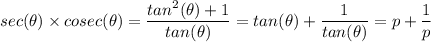
Explanation:
The given trigonometric relations are
tan(θ) = p
sec(θ)×cosec(θ) = p + 1/p
We note that, when tan(θ) = p, we have;
p + 1/p = tan(θ) + 1/(tan(θ)) = (tan²(θ) + 1)/tan(θ)
By trigonometric ratios, we have;
tan²(θ) + 1 = sec²(θ) =1/cos²(θ) which gives;
(tan²(θ) + 1)/tan(θ) = 1/cos²(θ) × 1/tan(θ) = cos(θ)/sin(θ)×1/cos²(θ)

Therefore;