Question

Jerry solved the system of equations. x minus 3 y = 1. 7 x + 2 y = 7. As the first step, he decided to solve for y in the second equation because it had the smallest number as a coefficient. Max told him that there was a more efficient way. What reason can Max give for his statement? The variable x in the first equation has a coefficient of one so there will be fewer steps to the solution. The variable x in the second equation has a coefficient of 7 so it will be easy to divide 7 by 7. The variable y in the second equation has a coefficient of 2 so it will be easy to divide the entire equation by 2. The variable x in the second equation has the largest coefficient. When dividing by 7, the solution will be a smaller number.

Answer 1

A: The variable x in the first equation has a coefficient of one so there will be fewer steps to the solution.

Explanation:

Answer 2

A. The variable x in the first equation has a coefficient of one so there will be fewer steps to the solution.

Explanation:

Given

`Equation\ 1: x - 3y = 1`

`Equation\ 2: 7x + 2y = 7`

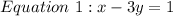
Required

Efficient way of solving the equations

The efficient way of solving this problem is by solving for x in the first equation because it has a coefficient of 1;

The evidence is shown as follows;

Make x the subject of formula in equation 1

`x = 1 + 3y`

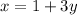
Substitute 1 + 3y for x in equation 2

`7x + 2y = 7`

`7(1 + 3y) + 2y = 7`

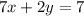
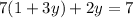
Open bracket

`7 + 21y + 2y = 7`

`7 + 23y =7`

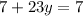
Make y the subject of formula

`23y = 7 - 7`

`23y = 0`

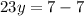
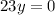
Divide both sides by 23

`(23y)/(23) = (0)/(23)`

`y = 0`

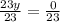
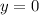
Recall that x = 1 + 3y

Substitute 0 for y in the above expression

`x = 1 + 3(0)`

`x = 1 + 0`

`x = 1`

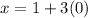
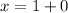
Solving for y in the second equation will take more steps